「我眼泪之中背负了所有在最深处的心情却无法说出口心中的痛别离的梦」

目前主要是开始重拾OI了。

题目主要以省选的基础算法题为主，高级算法或者数据结构的题目想想也可以。60天内做150道题目以上，最好能达到200道。

[GXOI/GZOI2019]旧词

题目描述

浮生有梦三千场
穷尽千里诗酒荒
徒把理想倾倒
不如早还乡

温一壶风尘的酒
独饮往事迢迢
举杯轻思量
泪如潮青丝留他方

——乌糟兽/愚青《旧词》

你已经解决了五个问题，不妨在这大树之下，吟唱旧词一首抒怀。最后的问题就是关于这棵树的，它的描述很简单。

给定一棵 $n$ 个点的有根树，节点标号 $1 \sim n$，$1$ 号节点为根。
给定常数 $k$。
给定 $Q$ 个询问，每次询问给定 $x,y$。
求：

$\sum\limits_{i \le x} \text{depth}(\text{lca}(i,y))^k$

$\text{lca}(x,y)$ 表示节点 $x$ 与节点 $y$ 在有根树上的最近公共祖先。
$\text{depth}(x)$ 表示节点 $x$ 的深度，根节点的深度为 $1$。
由于答案可能很大，你只需要输出答案模 $998244353$ 的结果。

输入输出格式

输入格式

输入包含 $n+Q$ 行。

第 $1$ 行，三个正整数 $n,Q,k$。

第 $i = 2 \sim n$ 行，每行有一个正整数 $f_i(1 \le f_i \le n)$，表示编号为 $i$ 的节点的父亲节点的编号。

接下来 $Q$ 行，每行两个正整数 $x,y(1 \le x,y \le n)$，表示一次询问。
输出格式

输出包含 $Q$ 行，每行一个整数，表示答案模 $998244353$ 的结果。

输入样例 #1
5 5 2
1
4
1
2
4 3
5 4
2 5
1 2
3 2
输出样例 #1
15
11
5
1
6

        说明
    ### 样例解释

输入的树：

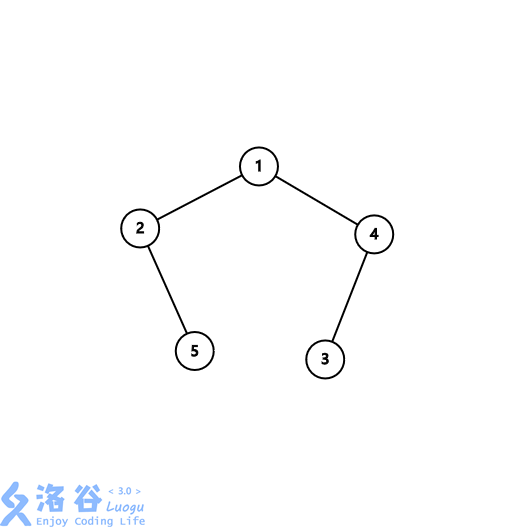
每个点的深度分别为 $1,2,3,2,3$。

第一个询问 $x = 4,y = 3$，容易求出：

$\text{lca}(1, 3) = 1,\text{lca}(2, 3) = 1,\text{lca}(3, 3) = 3,\text{lca}(4, 3) = 4$

于是 $\text{depth}(1)^2+\text{depth}(1)^2+\text{depth}(3)^2+\text{depth}(4)^2 = 1+1+9+4 = 15$。

测试点编号	$n$ 的规模	$Q$ 的规模	$k$ 的规模	约定
$1$	$n \le 2,000$	$Q \le 2,000$	$1 \le k \le 10^9$	无
$2$	$n \le 2,000$	$Q \le 2,000$	$1 \le k \le 10^9$	无
$3$	$n \le 2,000$	$Q \le 2,000$	$1 \le k \le 10^9$	无
$4$	$n \le 2,000$	$Q \le 2,000$	$1 \le k \le 10^9$	无
$5$	$n \le 50,000$	$Q \le 50,000$	$1 \le k \le 10^9$	存在某个点，其深度为 $n$
$6$	$n \le 50,000$	$Q \le 50,000$	$1 \le k \le 10^9$	存在某个点，其深度为 $n$
$7$	$n \le 50,000$	$Q \le 50,000$	$1 \le k \le 10^9$	存在某个点，其深度为 $n$
$8$	$n \le 50,000$	$Q \le 50,000$	$1 \le k \le 10^9$	存在某个点，其深度为 $n$
$9$	$n \le 50,000$	$Q = n$	$1 \le k \le 10^9$	对于第 $i$ 个询问，有 $x = i$
$10$	$n \le 50,000$	$Q = n$	$1 \le k \le 10^9$	对于第 $i$ 个询问，有 $x = i$
$11$	$n \le 50,000$	$Q \le 50,000$	$k = 1$	无
$12$	$n \le 50,000$	$Q \le 50,000$	$k = 1$	无
$13$	$n \le 50,000$	$Q \le 50,000$	$k = 2$	无
$14$	$n \le 50,000$	$Q \le 50,000$	$k = 2$	无
$15$	$n \le 50,000$	$Q \le 50,000$	$k = 3$	无
$16$	$n \le 50,000$	$Q \le 50,000$	$k = 3$	无
$17$	$n \le 50,000$	$Q \le 50,000$	$1 \le k \le 10^9$	无
$18$	$n \le 50,000$	$Q \le 50,000$	$1 \le k \le 10^9$	无
$19$	$n \le 50,000$	$Q \le 50,000$	$1 \le k \le 10^9$	无
$20$	$n \le 50,000$	$Q \le 50,000$	$1 \le k \le 10^9$	无

大概是联赛最难题的水平，开始思考。

首先前12个点没什么毛病，暴力+LCA那题思路。

13，14两个点相当于是$2k-1$的等差数列，也是可以的。

但是再高次，哪怕是3次都不是很好做了。

好吧想出来了。

一个月前做过一道题叫LCA，当时我用了一个巧妙的离线顺序用HPD解决了那道题。

然后这道题和那道题是一模一样的…..

思想就是更换算贡献的顺序但是依然等价。

但是还有一个难点，如何支持二操作呢？

想了一下LCA，发现我们实际上把深度转化成了路径上每个点都加一，然后求和正好就是答案，隐含了答案的可合并性，但这道题的$K$次幂和并不是那么好合并。。。

综上，我们获得了60~70分的好成绩，其实这个题比联赛最难题要难hhh。

突然我发现我想错了一个地方，注意到$k=1$的时候我们给每个点加一是因为$\sum 1 = dep_x$

那么利用差分的思想，给每个点加$dep^k x - dep^k fx$，根路径和正好是想要的，第二步其实写错了，因为那样做给每个询问的贡献变成了$\sum dep^k_i$，不是我们想要的。

具体怎么用线段树完成这个差分操作呢？新建序列$b{idx} = dep^k_x - dep^k{fx}$ , 原树根的$dep_{fx} = 0$.

对$b$求出前缀和数组$s$

然后HPD线段树每个更新区间节点$P[l,r]$时，可以$O(1)$获得加上的值为$s{r} - s{l-1}$

~~1小时轻松获得了本题的思路满分~~

先看Thomas Calculus了，代码看心情写吧，下一题也是GZOI2019，逼死强迫症。