Post 74

Veröffentlicht am

湛蓝色的初一，柠檬色的海。

上午教练找了些网络流的板子题,基本爆0嘻嘻.

下午51nod省选模拟赛,切了B拿了C的最高档暴力(除了分块qwq),A的暴力DP写不出来有点可惜.

其实懒得写

A 抽卡大赛

51Nod为了活跃比赛前的气氛，组织了场抽卡比赛。这场比赛共 nn个人参加，主办方根据非欧血统鉴定器，得到了一些数据。每个人抽卡有 MiMi 种可能，得到的卡能力值为 AijAij 代价为 GijGij 的可能性为 PijPij ，所谓代价指的是玩家需要将一轮比赛后所得的点头盾的 Gij% 交给主办方。每轮比赛每个人都随机抽取卡片，待全部人抽取完毕后进行排名（按照A从大到小排），排在第 ii 位的人有 ViVi 的点头盾收入。现在主办方想知道一轮比赛后每个人的期望收入。

输入

1
2
3
4
5
6
第一行一个正整数 n
接下来 n 个部分
每个部分第一行为正整数 Mi，接下来 Mi 行有三个整数 Aij Gij Pij
接下来一行 n 个整数，分别为 Vi
设 ∑Pij=Qi，则第 i 个人抽到第 j 张卡的概率为 Pij/Qi
1<=n,Mi<=200，1<=Aij<=1000000000，保证 Aij 互不相同，0<=Gij<=100，1<=Pij<=1000，1<=Vi<=1000

输出

1
2
输出 n 行，每行一个数表示每个人的期望收入
为了防止精度误差，输出答案在模 1e9+7 意义下的数值

输入样例

1
2
3
4
5
6
7
8
2
2
3 50 5
4 50 5
2
5 50 5
6 50 5
2 2

输出样例

1
2
1
1

题解

只会指数做法,暂时咕咕咕.

B 异或约数和

定义 f(i)f(i) 为 ii 的所有约数的异或和，给定 n(1≤n≤1014)n(1≤n≤1014) ，求 f(1) xor f(2) xor f(3) xor…xor f(n)f(1) xor f(2) xor f(3) xor…xor f(n) （其中xor表示按位异或）

样例解释：

$f(1) = 1$

$f(2) = 1 xor 2 = 3$

$f(3) = 1 xor 3 = 2$

$f(4) = 1 xor 2 xor 4 = 7$

$1 xor 3 xor 2 xor 7 = 7$

输入

1
一行，输入一个整数n

输出

1
一行，一个整数为答案

输入样例

1
4

输出样例

1
7

题解

先想了个最简单的$O(nlogn)$的暴力处理约数模拟一下,20多分.
然后正当我准备分段打表的时候,我突然想到这不就是所有1~n出现了多少次就xor多少次.
然后就是求

$Xor \sum_{i=1}^{n}[\biggl\lfloor\frac{n}{i}\biggr\rfloor mod 2]i$

然后就是$O(n)$ , 45

然后我们整除分块找找规律$O(logn)$求一下前缀异或,就是$O(\sqrt{n}logn)$ , 65

然后输出一下规律,发现可以$O(1)$前缀异或,$O(\sqrt{n})$ , AC

似乎逻辑非常清晰的一道题.

C 小朋友的笑话

小O是一个很萌很萌的女孩子。
有一天小O叫了很多很多萌萌哒小朋友到家里来玩。
由于太无聊了，她们开始讲笑话。
总共有N个小朋友排成一排，编号1~N。
在某个时刻，会有编号为xi的小朋友看到了笑话li，然后她会把这个笑话讲出来，与她距离不超过ki的小朋友都会听到这个笑话。
当一个小朋友听到一个笑话时，如果她是第一次听得到这个笑话，那么她会觉得这个笑话非常好笑，笑的停不下来。如果她听到之前就是在笑的她会继续笑。
如果她之前听过这个笑话，那么她会觉得这个笑话非常无聊，她会立即停止笑。

现在小O想知道，在某些时刻一段区间内有多少小朋友在笑。

输入

1
2
3
4
5
第一行两个整数N,M，表示小朋友的数量和事件数量，(1<=N,M<=100000)
接下来M行
第一行为一个正整数op（1<=op<=2），表示事件类型。
如果op=1，接下来三个整数xi li ki，表示该时间点小朋友xi(1<=xi<=N)讲了一个笑话li(1<=li<=100000)，传播距离为ki(0<=ki<=N)。
如果op=2，接下来两个整数l r，表示该时间点小O想知道区间[l,r]中有多少小朋友在笑(1<=l<=r<=N)

输出

1
对每个询问操作，输出答案

输入样例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
10 14
1 3 11 0
2 3 3
1 3 11 2
2 1 5
1 5 12 1
2 4 6
1 8 13 2
2 6 10
1 7 11 2
2 5 9
1 10 12 1
2 9 11
1 9 12 0
2 1 10

输出样例

1
2
3
4
5
6
7
1
4
3
5
4
2
7

题解

暂时只会一个bitset暴力,本来想口胡一个CDQ分治的做法结果失败了….

暴力给每个人维护一个听过的桶.只需要把桶用bitset就可以加快一点速度,拿到24分.

感觉这题挺有意思,改天写下.

最大密度子图

题意: 给你一组点,点有点权,一组边,边有边权.可以选定一组点集,端点都在其中的边将被选中,设边权之和为$\sum E$,点权之和为$\sum V $, 请求出最大的$\frac{\sum E}{\sum V}$

数据范围是Dinic接受范围.

题解

Emmmmm据说在郑州学过,可是发高烧的我根本没学会啥……

这种题可以使用最小割模型.

img

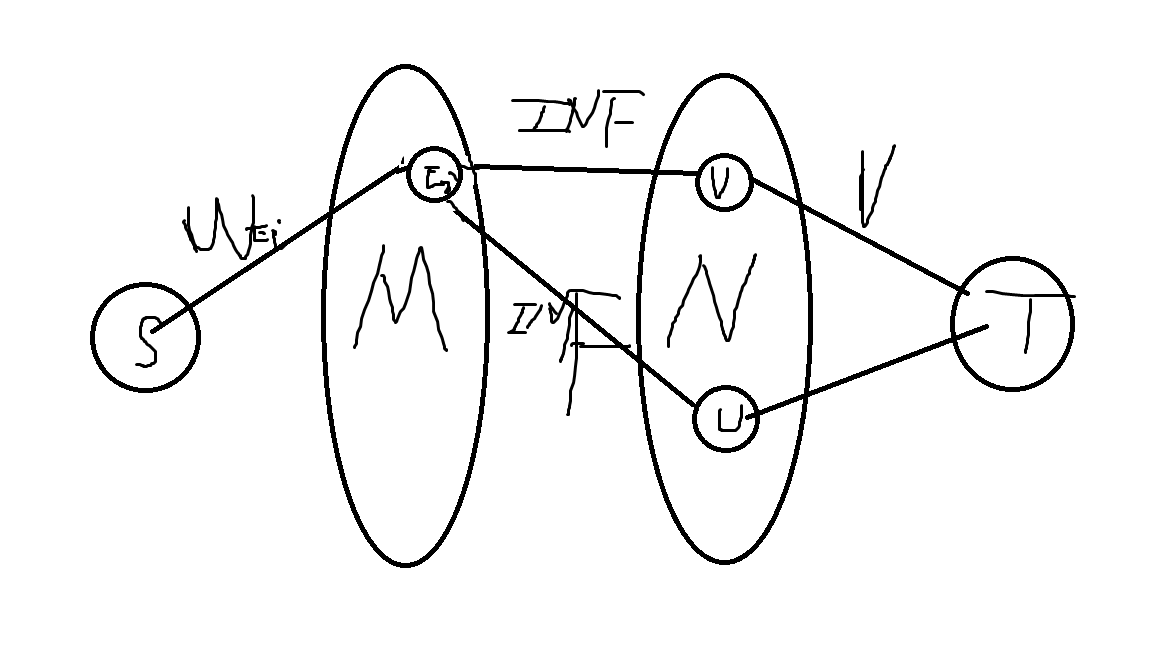
就像上面那样 , 我们从源点向每个代表边的点连一个边权的流量,然后边的点分别向两个端点连INF边表示不能割掉,然后那些代表原图中点的点向汇点连点权乘比值(0/1分数规划)

注意乘比值!!

然后我感觉从这个啥也没学到,甚至不怎么理解为什么这么做很正确.

真是尴尬.

分治FFT看完也来不及写了

明天补完锅好了.