Post 71

Veröffentlicht am | Edited on

今天好像挺垃圾的啊。

时间背着我悄悄捏碎从前。

感觉lzj被从我开创的新文学玩坏了哈哈哈哈哈

https://challestend.github.io/chaoyu/

[USACO17DEC]Standing Out from the Herd

题目描述

Just like humans, cows often appreciate feeling they are unique in some way. Since Farmer John’s cows all come from the same breed and look quite similar, they want to measure uniqueness in their names.

Each cow’s name has some number of substrings. For example, “amy” has substrings {a, m, y, am, my, amy}, and “tommy” would have the following substrings: {t, o, m, y, to, om, mm, my, tom, omm, mmy, tomm, ommy, tommy}.

A cow name has a “uniqueness factor” which is the number of substrings of that name not shared with any other cow. For example, If amy was in a herd by herself, her uniqueness factor would be 6. If tommy was in a herd by himself, his uniqueness factor would be 14. If they were in a herd together, however, amy’s uniqueness factor would be 3 and tommy’s would be 11.

Given a herd of cows, please determine each cow’s uniqueness factor.

定义一个字符串的「独特值」为只属于该字符串的本质不同的非空子串的个数。如 “amy” 与 “tommy” 两个串，只属于 “amy” 的本质不同的子串为 “a” “am” “amy” 共 3 个。只属于 “tommy” 的本质不同的子串为 “t” “to” “tom” “tomm” “tommy” “o” “om” “omm” “ommy” “mm” “mmy” 共 11 个。 所以 “amy” 的「独特值」为 3 ，”tommy” 的「独特值」为 11 。

给定 N (N \leq 10^5N≤105) 个字符集为小写英文字母的字符串，所有字符串的长度和小于 10^5105，求出每个字符串「独特值」。

输入输出格式

输入格式：

The first line of input will contain $N$ ($1 \le N \le 10^5$). The following N lines will each contain the name of a cow in the herd. Each name will contain only lowercase characters a-z. The total length of all names will not exceed $10^5$

输出格式：

Output NN numbers, one per line, describing the uniqueness factor of each cow.

输入输出样例

输入样例#1：

1
2
3
4
3
amy
tommy
bessie

输出样例#1：

1
2
3
3
11
19

题解

一道不算难的SA/SAM题结果我没调出来。。。

想出做法不算难，画图（画图很重要）

读完题发现除了在原有去重的情况下，还需要去掉一些情况，就是不同串的LCP（两个串的答案都要去掉这部分）。

我们发现后缀全排完序后可以用这种情况来代表典型情况：

img

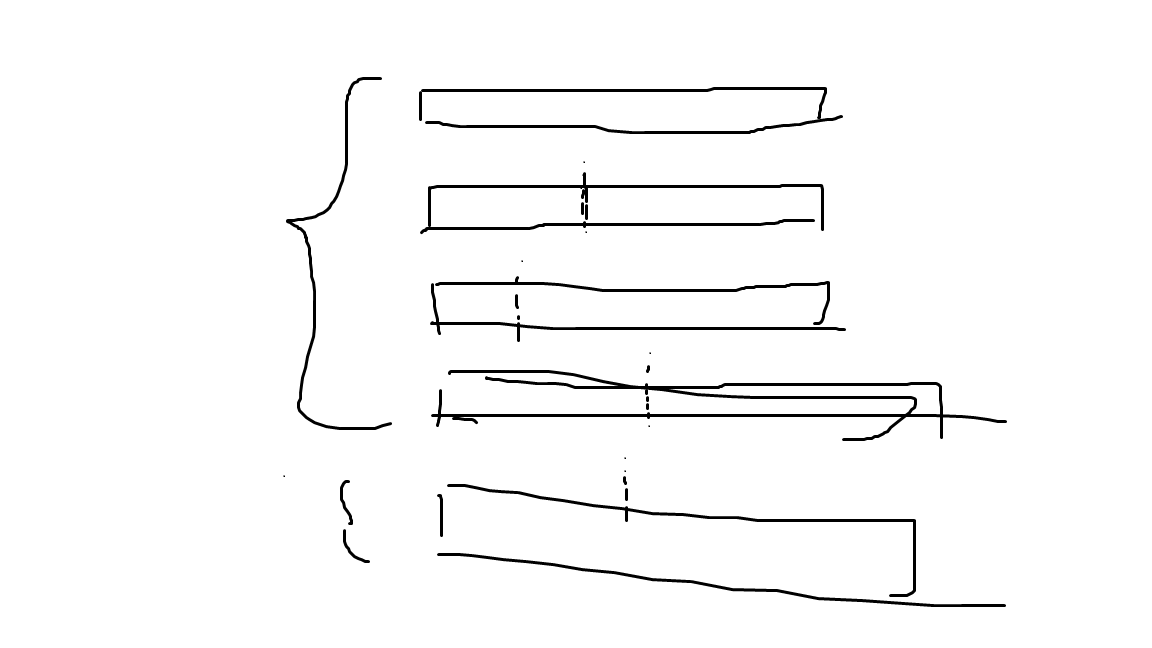
大括号表示同一个字符串。

我们在处理完同一个串的本质不同子串并统计完答案后，后面来了一个不同的后缀$T$。

我们能不能直接减掉最下面的那个$h_i$的值呢？

不能，因为我们实际上多减了上面那一段的最小值，把那一段加回来就统计正确了。

可能你还是不明白？

这个值是由最小值和它下面到这个不同串$T$所要去掉的拼起来的！

假设那个最小值的位置是$pos$.

$pos$上面的某个串$k$和它的上面的LCP即$h_rk{k}$肯定大于等于和$T$的LCP，所以就不用减了。这是关于最小值前面和它同串的正确性。

最小值后面的那些，贡献是一点一点合起来的。像这样。

img

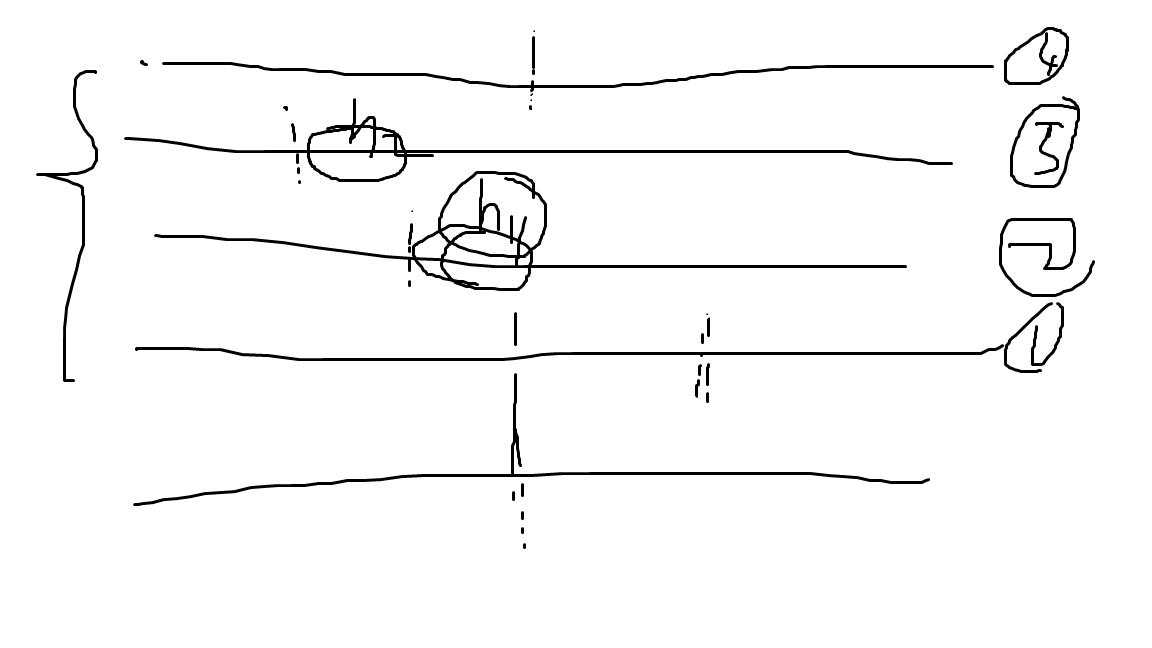
如果$h$不单调递减，我们就把那些不递减的去掉，因为那些不递减的在字符串内部去重统计就去掉了。
对于递减的就像我画的，减去的是$h_1+h_2$，这些合起来就是排名$k$后缀$T$的$h_k$减去这组连续同串后缀最小值。
这样统计出了这部分后缀正确的独特本质不同子串。

注意开闭问题，时刻考虑$h$数组定义为$hi = lcp(sa_i,sa{i-1})$

(我觉得有人肯定说我SA平凡性质要啰嗦半天，我经常被wzx嘲讽)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
#include <cstdio>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <cstring>
#define maxn 200005
int id[maxn] , sa[maxn] , rk[maxn] , c[maxn] , h[maxn] , pos[maxn] , n , m , ct , mns[maxn] , s[maxn];
inline void sort()
{
	for(int i = 1 ; i <= m ; ++i) c[i] = 0;
	for(int i = 1 ; i <= ct ; ++i) ++c[rk[pos[i]]];
	for(int i = 1 ; i <= m ; ++i) c[i] += c[i-1];
	for(int i = ct ; i >= 1 ; --i) sa[c[rk[pos[i]]]--] = pos[i];
}

inline void SA()
{
	for(int i = 1 ; i <= n ; ++i)
		pos[i] = i , rk[i] = s[i];
	ct = n , m = 200000;
	sort();
	for(int k = 1 ; k <= n ; k <<= 1)
	{
		ct = 0;
		for(int i = 1 ; i <= k ; ++i)	pos[++ct] = n - k + i;
		for(int i = 1 ; i <= n ; ++i) if(sa[i] > k) pos[++ct] = sa[i] - k;
		sort();
		std::swap(rk , pos);
		rk[sa[1]] = ct = 1;
		for(int i = 2 ; i <= n ; ++i)
			rk[sa[i]] = (pos[sa[i]] == pos[sa[i-1]] && pos[sa[i] + k] == pos[sa[i-1] + k]) ? ct : ++ct;
		if((m = ct) == n) break;
	}
	int k = 0;
	for(int i = 1 ; i <= n ; ++i)
	{
		if(k) --k;
		for(int p = sa[rk[i]-1] ; s[i + k] == s[p + k] ; ++k);
		h[rk[i]] = k;
	}
}

int l[maxn] , r[maxn] , t;
inline void read(int num)
{
	l[num] = n + 1 ;
	char ch = getchar();
	while(ch < 'a' || ch > 'z') ch = getchar();
	while(ch >= 'a' && ch <= 'z') id[++n] = num , s[n] = ch , ch = getchar();
	r[num] = n;
	s[++n] = 'z' + num;
}

long long ans[maxn];

inline void solve()
{
	int mn = 0;
//	for(int i = 1 ; i <= n ; ++i)
//		printf("%d %d\n",s[sa[i]],s[sa[i]+1]);
//	return ;
	for(int i = 1 ; i <= n ; ++i)
	{
		int p = id[sa[i]];
		ans[p] += r[p] - sa[i] + 1 - h[i];
		mn = std::min(mn , h[i]);
		if(p != id[sa[i-1]]) ans[id[sa[i-1]]] -= h[i] , ans[id[sa[i-1]]] += mn , mn = h[i];		
	}

}


int main()
{
//	freopen("data.in","r",stdin);
	scanf("%d",&t);
	for(int i = 1 ; i <= t ; ++i) read(i);
	SA();
	solve();
	for(int i = 1 ; i <= t ; ++i)
		printf("%lld\n",ans[i]);
}

下午胡策，就会两题部分分非常自闭（暂时第3？？）

（D题懒得打暴力，反正比不上wzx和shzr两个切题大佬qwq）

艹我要是会多项式算法就轻松爆切T1啊啊啊啊。

T1我甚至能口胡出$O(nlog^2n)$的做法qwq。

部分分也调了半天，很多智障细节又卷土重来了，各种组合数写错.jpg

我TM今晚就学会多项式全家桶——IMist

潮队爷lzj又开始潮了！！！

img

我来写一写我写的部分分吧qwq。

A. 「Croi0001T1」Challestend and Hyperrectangle

题目背景

idea/题面/思路/std/数据：\color{red}\mathsf{rehtorbegnaro}rehtorbegnaro

题目描述

Challestend有一个高维立方体。

这个立方体是$n$维的，它的nn个边长分别是$a{1},a{2},\cdots,a{n}$。一开始整个立方体都是白色的。现在Challestend给这个立方体的表面涂上了一层黑色，然后将它切成了$\prod{i=1}^{n}a_{i}$个边长都是$1$的小立方体。

一个很明显的事实是，这些小立方体被涂成黑色的面数不一定相等。立方体$2^{n}$个顶点处的小立方体可能有$n$面被涂成黑色，完全在内部的小立方体可能还是白色。

现在Challestend想知道，对于$[0,2n]$上的每一个整数$i$，有多少个小立方体恰有$i$面被涂成黑色。因为答案可能会很大，他只想知道其对$998244353$取模的结果。

输入格式

第一行包含一个整数nn。

第二行包含nn个整数，分别是$a{1},a{2},\cdots,a_{n}$

输出格式

仅一行，包含$2n+1$个整数，第$i$个整数表示有多少个小立方体恰有$i-1$面被涂成黑色。对$998244353$取模。

样例数据

样例输入1
1
2
4
3 3 5 6
样例输出1
1
12 62 108 72 16 0 0 0 0
样例输入2
1
2
20
562788232015521615 10636209524447908031 7115845897112471457 13797915605844231623 15162584865945819082 6956504350961808511 1786109578779773898 12538232916278239980 1871352631905881904 17482854226847293687 1321867384284731203 2196021990878082265 14173657558977763067 8860233270423555484 9971406497596149470 10592911097040324745 3776841115747389372 13446413960515438456 636053243107690483 4224161609805282571
样例输出2
1
128856859 15533937 115747763 600656594 191159922 943031353 601067786 416384022 881090790 814502150 264166330 107454484 484474772 856916898 486327280 439770255 795221682 48327188 279518607 232059473 1048576 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
样例输入3
1
2
10
156498 19484195 59419841918 941949894 998244354 1 5145498 564654654 91791879 645149879879
样例输出3
1
0 0 562549386 55070731 864082510 25560817 756434845 726990475 413572809 753698164 336464529 512 0 0 0 0 0 0 0 0 0
样例输入4
1
2
10
9982443531 9982443531 9982443531 9982443531 9982443531 9982443531 9982443531 9982443531 9982443531 9982443531
样例输出4
1
1 998244333 180 998243393 3360 998236289 13440 998228993 11520 998239233 1024 0 0 0 0 0 0 0 0 0 0

数据范围与约定

时空限制：1\text{s}/128\text{MB}1s/128MB

对于20\%20%的数据，$n\leqslant 20$

对于另外20\%20%的数据，所有a_{i}a**i相等。

对于100\%100%的数据，$4\leqslant n\leqslant 30000$，$1\leqslant a_{i}\lt 2^{64}$

数据（很罕见地）有梯度。

题解

首先我们需要胡乱分析一下这道题。

我们根本不知道高于4维的几何体是什么样子的

我们可以理性胡想来考虑它的性质（从三维推广到任意维度，不会证明（对不对都不知道））

我到现在连Tesseract都不知道是怎么回事
首先染了$n$面的小正方体是在“棱角上”，任意维度下一个立方体有多少个顶点呢？
$2^n$ , 并不会证明.jpg

其实Wiki里有个关于这个的解释如下：
The construction of hypercubes can be imagined the following way:

1-dimensional: Two points A and B can be connected to become a line, giving a new line segment AB.
2-dimensional: Two parallel line segments AB and CD can be connected to become a square, with the corners marked as ABCD.
3-dimensional: Two parallel squares ABCD and EFGH can be connected to become a cube, with the corners marked as ABCDEFGH.
4-dimensional: Two parallel cubes ABCDEFGH and IJKLMNOP can be connected to become a tesseract, with the corners marked as ABCDEFGHIJKLMNOP.

所以每增加一维顶点数翻倍。

那么一个面都没有染色的呢？

在三维下是$(a-1)(b-1)(c-1)$，由样例可知高维也是如此。

然后发现每一项都有2的次幂？提出来凭着一点敏锐的观察力发现对于染色数为$k$的就是：

$2^k\sum\prod{i1~i{n-k}}a_i$

至于怎么证明并不重要（不会）

都相同可以用组合数计算。

对于全部数据，据说std是$O(n^2)$的。。。

[USACO06DEC]牛奶模式Milk Patterns

题目描述

Farmer John has noticed that the quality of milk given by his cows varies from day to day. On further investigation, he discovered that although he can’t predict the quality of milk from one day to the next, there are some regular patterns in the daily milk quality.

To perform a rigorous study, he has invented a complex classification scheme by which each milk sample is recorded as an integer between 0 and 1,000,000 inclusive, and has recorded data from a single cow over N (1 ≤ N ≤ 20,000) days. He wishes to find the longest pattern of samples which repeats identically at least K (2 ≤ K ≤ N) times. This may include overlapping patterns — 1 2 3 2 3 2 3 1 repeats 2 3 2 3 twice, for example.

Help Farmer John by finding the longest repeating subsequence in the sequence of samples. It is guaranteed that at least one subsequence is repeated at least K times.

农夫John发现他的奶牛产奶的质量一直在变动。经过细致的调查，他发现：虽然他不能预见明天产奶的质量，但连续的若干天的质量有很多重叠。我们称之为一个“模式”。 John的牛奶按质量可以被赋予一个0到1000000之间的数。并且John记录了N(1<=N<=20000)天的牛奶质量值。他想知道最长的出现了至少K(2<=K<=N)次的模式的长度。比如1 2 3 2 3 2 3 1 中 2 3 2 3出现了两次。当K=2时，这个长度为4。

输入输出格式

输入格式：

Line 1: Two space-separated integers: N and K

Lines 2..N+1: N integers, one per line, the quality of the milk on day i appears on the ith line.

输出格式：

Line 1: One integer, the length of the longest pattern which occurs at least K times

输入输出样例

输入样例#1：

1
2
3
4
5
6
7
8
9
8 2
1
2
3
2
3
2
3
1

输出样例#1：

1
4

题解

这道题由于我是按标签“二分答案”搜的，所以就秒了。。。

二分长度$l$，看看有没有一个$h$上的区间长度大于等于$k-1$并且每个元素都大于等于$l$.

时间复杂度$O(nlogn)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#include <map>
#define maxn 40005

int sa[maxn] , rk[maxn] , pos[maxn] , c[maxn] , h[maxn] , n , m , ct , k , s[maxn];

inline void sort()
{
	for(int i = 1 ; i <= m ; ++i) c[i] = 0;
	for(int i = 1 ; i <= ct ; ++i) ++c[rk[pos[i]]];
	for(int i = 1 ; i <= m ; ++i) c[i] += c[i-1];
	for(int i = ct ; i >= 1 ; --i) sa[c[rk[pos[i]]]--] = pos[i];
}

inline void SA()
{
	for(int i = 1 ; i <= n ; ++i)
		pos[i] = i , rk[i] = s[i];
	m = ct = n;
	sort();
	for(int k = 1 ; k <= n ; k <<= 1)
	{
		ct = 0;
		for(int i = 1 ; i <= k ; ++i) pos[++ct] = n - k + i;
		for(int i = 1 ; i <= n ; ++i) if(sa[i] > k) pos[++ct] = sa[i] - k;
		sort();
		std::swap(rk,pos);
		rk[sa[1]] = ct = 1;
		for(int i = 2 ; i <= n ; ++i)
			rk[sa[i]] = (pos[sa[i]] == pos[sa[i-1]] && pos[sa[i] + k] == pos[sa[i-1] + k]) ? ct : ++ct;
		if((m = ct) == n) break;
	}
	int k = 0;
	for(int i = 1 ; i <= n ; ++i)
	{
		if(k) --k;
		for(int p = sa[rk[i]-1] ; s[i+k] == s[p+k] ; ++k);
		h[rk[i]] = k;
	}
}

struct Node{
	int val , num;
	bool operator < (const Node& x)const{
		return val < x.val;
	}
}p[maxn];
inline void unique()
{
	for(int i = 1 ; i <= n ; ++i)
		p[i] = (Node){s[i],i};
	std::sort(p+1,p+n+1);
	int rev = 0;
	for(int i = 1 ; i <= n ; ++i)
	{
		if(p[i].val != p[i-1].val) ++rev;
		s[p[i].num] = rev;
	}
}

inline bool solve(int len)
{
	int ln = 0;
	for(int i = 1 ; i <= n ; ++i)
	{
		if(h[i] >= len) ++ln;
		else ln = 0;
		if(ln == k-1)  return true;
	}
	return false;
}
int main()
{
	scanf("%d%d",&n,&k);
	for(int i = 1 ; i <= n ; ++i)
		scanf("%d",&s[i]);
	unique();
	SA();
	int l = 0 , r = n , ans = 0;
	while(l <= r)
	{
		int mid = l + r >> 1;
		if(solve(mid)) ans = mid , l = mid + 1;
		else r = mid - 1;
	}
	printf("%d",ans);
}

恩就这样。

美好的每一天~不连续的存在~

题目描述

音无彩名给了你一棵n个节点的树，每个节点有一种颜色，有m次查询操作

查询操作给定参数l r x，需输出：

将树中编号在[l,r]内的所有节点保留，x所在联通块中颜色种类数

每次查询操作独立

输入输出格式

输入格式：

第一行两个数n，m

第二行n个数表示每个节点的颜色

之后n-1行，每行两个数x和y，表示x和y之间连有一条边

之后m行，每行三个数l r x，表示一次查询操作

输出格式：

对每个查操作，输出一行一个数表示答案

输入输出样例

输入样例#1：

1
2
3
4
5
6
7
8
9
10
5 4
1 3 5 3 5
1 2
2 3
3 4
4 5
1 5 1
2 4 3
3 4 3
1 4 3

输出样例#1：

1
2
3
4
3
2
2
3

说明

对于100%的数据，所有出现过的数在[0,100000]之间

题解

好像直接按照编号分块就好了吧。

每个块维护一个颜色的bitset。

$O(n^2/w)$

不大靠谱。

正解是点分树+主席树，非常牛逼的样子。

[USACO18DEC]Sort It Out

题意概要：给定一个长为$n$的排列，可以选择一个集合$S$使这个集合内部元素排到自己在整个序列中应该在的位置（即对于集合$S$内的每一个元素$i$，使其排到第$i$号位置，使得整个排列在排序后（指的是这样操作后）为上升序列。求满足这样条件的，且集合大小最小的集合中字典序第$k$小的集合（可能总结不到位，看原题面吧）

$n\leq 10^5$

题解

读题2分钟后终于明白意思。。。。

暂时咕咕咕