一场非常丢人的CF。(某种意义上是我认真打的第一场…)

T1 , T2并没有什么心情写。

~~成为划水选手和搬砖翻译。。。。~~

C. Birthday

Cowboy Vlad has a birthday today! There are nn children who came to the celebration. In order to greet Vlad, the children decided to form a circle around him. Among the children who came, there are both tall and low, so if they stand in a circle arbitrarily, it may turn out, that there is a tall and low child standing next to each other, and it will be difficult for them to hold hands. Therefore, children want to stand in a circle so that the maximum difference between the growth of two neighboring children would be minimal possible.

Formally, let’s number children from 11 to nn in a circle order, that is, for every ii child with number ii will stand next to the child with number i+1i+1, also the child with number 11 stands next to the child with number nn. Then we will call the discomfort of the circle the maximum absolute difference of heights of the children, who stand next to each other.

Please help children to find out how they should reorder themselves, so that the resulting discomfort is smallest possible.

Input

The first line contains a single integer nn (2≤n≤1002≤n≤100) — the number of the children who came to the cowboy Vlad’s birthday.

The second line contains integers a1,a2,…,ana1,a2,…,an (1≤ai≤1091≤ai≤109) denoting heights of every child.

Output

Print exactly nn integers — heights of the children in the order in which they should stand in a circle. You can start printing a circle with any child.

If there are multiple possible answers, print any of them.

Examples

input

Copy

1 2	5 2 1 1 3 2

output

Copy

1 2 3 2 1

input

Copy

1 2	3 30 10 20

output

Copy

10 20 30

Note

In the first example, the discomfort of the circle is equal to 11, since the corresponding absolute differences are 11, 11, 11 and 00. Note, that sequences [2,3,2,1,1][2,3,2,1,1] and [3,2,1,1,2][3,2,1,1,2] form the same circles and differ only by the selection of the starting point.

In the second example, the discomfort of the circle is equal to 2020, since the absolute difference of 1010 and 3030 is equal to 2020.

题解

看到数据范围你肯定没有料到这题是$O(n)$的。

丢人.jpg

构造。

按照从小到大往序列一个左边一个右边加就好了。

为什么是正确的呢？给出一个简短的证明：

由于答案是$\max{a{i+2}-a{i}}$

我们证明对于原序列，对于任意$i$ , $a_{i+2}-a_i$ , 都有答案不小于它。

将每个元素看成一个点，我们要做的是找一个Hamilton环，使得最大边最小。对于那些大于$a_{i+2} - a_i$的边，我们把它删去，如图。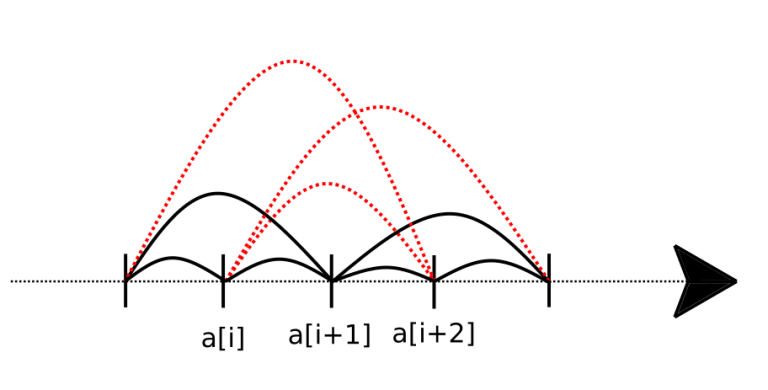

然后图中出现了割点，不可能存在Hamilton环，也就是说对于任意$i$答案不可能小于$a{i+2}-a_i$，因此答案就是$\max{a{i+2}-a_i}$，具体构造用上述方法即可。

Code:

#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#define maxn 105
int n , a[maxn] , c[maxn];
bool cmp(int x, int y){
	return x > y;
}

int main()
{
	scanf("%d",&n);
	for(int i = 1 ; i <= n ; ++i)
		scanf("%d",&a[i]);
	std::sort(a + 1 , a + n + 1);
	int l = 1 , r = n;
	for(int i = 1 ; i <= n ; ++i)
	{
		if(i & 1) c[l++] = a[i];
		else c[r--] = a[i];
	}
	for(int i = 1 ; i <= n ; ++i)
		printf("%d ",c[i]);
}

D. Gourmet choice

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Mr. Apple, a gourmet, works as editor-in-chief of a gastronomic periodical. He travels around the world, tasting new delights of famous chefs from the most fashionable restaurants. Mr. Apple has his own signature method of review — in each restaurant Mr. Apple orders two sets of dishes on two different days. All the dishes are different, because Mr. Apple doesn’t like to eat the same food. For each pair of dishes from different days he remembers exactly which was better, or that they were of the same quality. After this the gourmet evaluates each dish with a positive integer.

Once, during a revision of a restaurant of Celtic medieval cuisine named «Poisson», that serves chestnut soup with fir, warm soda bread, spicy lemon pie and other folk food, Mr. Apple was very pleasantly surprised the gourmet with its variety of menu, and hence ordered too much. Now he’s confused about evaluating dishes.

The gourmet tasted a set of nn dishes on the first day and a set of mm dishes on the second day. He made a table aa of size n×mn×m, in which he described his impressions. If, according to the expert, dish ii from the first set was better than dish jj from the second set, then aijaij is equal to “>”, in the opposite case aijaij is equal to “<”. Dishes also may be equally good, in this case aijaij is “=”.

Now Mr. Apple wants you to help him to evaluate every dish. Since Mr. Apple is very strict, he will evaluate the dishes so that the maximal number used is as small as possible. But Mr. Apple also is very fair, so he never evaluates the dishes so that it goes against his feelings. In other words, if aijaij is “<”, then the number assigned to dish ii from the first set should be less than the number of dish jj from the second set, if aijaij is “>”, then it should be greater, and finally if aijaij is “=”, then the numbers should be the same.

Help Mr. Apple to evaluate each dish from both sets so that it is consistent with his feelings, or determine that this is impossible.

Input

The first line contains integers nn and mm (1≤n,m≤10001≤n,m≤1000) — the number of dishes in both days.

Each of the next nn lines contains a string of mm symbols. The jj-th symbol on ii-th line is aijaij. All strings consist only of “<”, “>” and “=”.

Output

The first line of output should contain “Yes”, if it’s possible to do a correct evaluation for all the dishes, or “No” otherwise.

If case an answer exist, on the second line print nn integers — evaluations of dishes from the first set, and on the third line print mmintegers — evaluations of dishes from the second set.

Examples

input

Copy

3 4
>>>>
>>>>
>>>>

output

Copy

1
2
3

Yes
2 2 2 
1 1 1 1

input

Copy

3 3
>>>
<<<
>>>

output

Copy

1
2
3

Yes
3 1 3 
2 2 2

input

Copy

3 2
==
=<
==

output

Copy

No

Note

In the first sample, all dishes of the first day are better than dishes of the second day. So, the highest score will be 22, for all dishes of the first day.

In the third sample, the table is contradictory — there is no possible evaluation of the dishes that satisfies it.

题解

这其实是sb题，但是要看你实现优不优美。。。。。

题意就是让你求两个序列，其中任意一对元素的大小关系都给定了，问你怎么填让最大值最小。。

显然这是个完全二分图求最长链，和DAG没有什么区别，求得时候把路径上每个点都填一下（更新最大值）

所以不知道为啥我拓扑就是过不去，然后抄袭魏老师改成DFS就过了。

然后魏老师表示这也许是$O(n^3)$的，我想了一下发现一个细节决定了它是不是$O(N^2)$….

假如DFS当前长度大于当前点被更新的最长链长度才返回，那就是$O(n^3)$….

假如加上等于，就是$O(N^2)$..

T与不T的差别就是这么小。。

最简单的一个肯定不严格的上界分析：

对于一个点，假设到达它严格大于它的最大值才返回，那么很可能有$O(n)$个点。

假设大于等于它都返回的话