下午愣是没写出一道基本的记忆化搜索题。。。

「LibreOJ NOIP Round #1」旅游路线

题目描述

T 城是一个旅游城市，具有 nn 个景点和 mm 条道路，所有景点编号为 1,2,…,n1,2,…,n。每条道路连接这 nn 个景区中的某两个景区，道路是单向通行的。每条道路都有一个长度。

为了方便旅游，每个景点都有一个加油站。第 ii 个景点的加油站的费用为 p_ip**i，加油量为 c_ic**i。若汽车在第 ii 个景点加油，则需要花费 p_ip**i 元钱，之后车的油量将被加至油量上限与 c_ic**i中的较小值。不过如果加油前汽车油量已经不小于 c_ic**i，则不能在该景点加油。

小 C 准备来到 T 城旅游。他的汽车油量上限为 CC。旅游开始时，汽车的油量为 00。在旅游过程中：

1、当汽车油量大于 00 时，汽车可以沿从当前景区出发的任意一条道路到达另一个景点（不能只走道路的一部分），汽车油量将减少 11；

2、当汽车在景点 ii 且当前油量小于 c_ic**i 时，汽车可以在当前景点加油，加油需花费 p_ip**i 元钱，这样汽车油量将变为 \min\{c_i,C\}min{c**i,C}。

一次旅游的总花费等于每次加油的花费之和，旅游的总路程等于每次经过道路的长度之和。注意多次在同一景点加油，费用也要计算多次，同样地，多次经过同一条道路，路程也要计算多次。

小 C 计划旅游 TT 次，每次旅游前，小 C 都指定了该次旅游的起点和目标路程。由于行程不同，每次出发前带的钱也不同。为了省钱，小 C 需要在旅游前先规划好旅游路线（包括旅游的路径和加油的方案），使得从起点出发，按照该旅游路线旅游结束后总路程不小于目标路程，且剩下的钱尽可能多。请你规划最优旅游路线，计算这 TT 次旅游每次结束后最多可以剩下多少钱。

输入格式

输入第一行包含四个正整数 nn，mm，CC，TT，每两个整数之间用一个空格隔开，分别表示景点数、道路数、汽车油量上限和旅行次数。

接下来 nn 行，每行包含两个正整数 p_ip**i，c_ic**i，每两个整数之间用一个空格隔开，按编号顺序依次表示编号为 1,2,…,n1,2,…,n 的景点的费用和油量。

接下来 mm 行，每行包含三个正整数 a_ia**i，b_ib**i，l_il**i，每两个整数之间用一个空格隔开，表示一条从编号为 a_ia**i 的景点到编号为 b_ib**i 的景点的道路，道路的长度为 l_il**i。保证 a_i\ne b_ia**i̸=b**i，但从一个景点到另一个景点可能有多条道路。

最后 TT 行，每行包含三个正整数 s_is**i，q_iq**i，d_id**i，描述一次旅游计划，旅游的起点为编号为 s_is**i 的景点，出发时带了 q_iq**i 元钱，目标路程为 d_id**i。

输出格式

输出 TT 行，每行一个整数，第 ii 行的整数表示第 ii 次旅游结束后最多剩下多少元钱。如果旅游无法完成，也就是说不存在从景点 s_is**i 出发用不超过 q_iq**i 元钱经过不小于 d_id**i 的路程的路线，则该行输出 -1−1。

样例

样例输入 1

样例输出 1

1
2

2
-1

样例解释

T 城的景区和道路如下图所示：

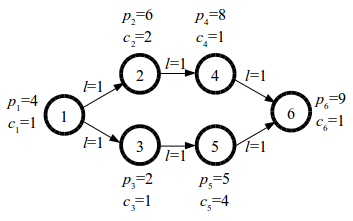
由图可知，从景点 11 出发，路程为 33 的路线有两条：1\rightarrow 2\rightarrow 4\rightarrow 61→2→4→6 和 1\rightarrow 3\rightarrow 5\rightarrow 61→3→5→6。

第 11 次旅游，最优路线为先在景点 11 加油，花费 44 元，此时油量为 11，然后到景点 22，此时油量为 00，在景点 22 加油，花费 66 元，此时油量为 22，接着到景点 44，此时油量为 11，最后到景点 66，总路程为 33，最后剩余 12-4-6=212−4−6=2 元。

第 22 次旅游，只用 99 元无论如何也无法走 33 的路程，因此旅游无法完成。

样例 2

见附加文件（在页面上方下载）中的选手目录下的 trip2.in 与 trip2.ans。

数据范围与提示

所有测试数据的范围和特点如下表所示：

测试点编号	nn	mm	CC	TT	p_i, \ c_ip*i, c*i	特殊性质
1	\le 10≤10	=n-1=n−1	\le 10≤10	=1=1	\le 10≤10	1, 2
2	\le 10≤10
3
4
5	=10=10	=10=10	2
6	=15=15	=15=15	\le 20≤20
7	=20=20	=20=20
8	\le 100≤100	=n-1=n−1	\le 10^3≤103	\le 50≤50	\le 100≤100	1, 3
9
10
11	\le 40≤40	\le 400≤400	3
12
13	\le 60≤60	\le 600≤600	\le 10^3≤103	无
14
15	\le 80≤80	\le 800≤800
16	\le 10^5≤105	\le 10^3≤103	\le 10^5≤105
17	\le 90≤90	\le 900≤900
18
19	\le 100≤100	\le 1000≤1000
20	\le 10^5≤105

其中，“特殊性质”一列中的数字意义如下：

特殊性质 1：所有 a_i=ia**i=i，b_i=i+1b**i=i+1，l_i=1l**i=1。
特殊性质 2：所有 d_i\le 10^3d**i≤103。
特殊性质 3：所有 q_i\le 100q**i≤100。

对于所有数据，$2\le n\le 100，1\le m\le 1000,1\le C,T\le 10^5$

题解

懒得修题面，凑合着看。

这道题一个超时的记忆化搜索不难想。~~（我今天下午可能在休眠。。。。）~~

设$f_{s,C,t}$表示起点为$s$，剩余金钱为$t$，汽车剩余油量为$C$.

并不需要记录中途的点，浪费了空间每次询问还得枚举，非常睿智~~（所以我一开始还是加上了记录当前点）~~。

然后这样算着点开数组，就能拿到60分，似乎不难。

然后写了半天。。

枚举答案和二分答案是一样的，复杂度瓶颈并不在这。（这个鬼复杂度真难算，影响复杂度的变量真TM多）

复杂度的瓶颈显然是DP过程，为$O(nCmax_{q_i}+Tq_i)$

然后上一下我写的程序，感觉今天下午完全没有状态（雾

写着写着连自己写什么都忘了，每次查询连枚举答案都没有，直接交了个源点跑值是多少就是多少。。。

Code：

#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#include <vector>
#include <cstring>
#define maxn 65
#define maxc 605
int n , m , C , T , f[maxn][maxc][maxc] , p[maxn] , c[maxn];
std::vector<int> g[maxn] , d[maxn];
int dp(int now , int r , int cur) //current point , remain money , remain oil
{
	if(f[now][r][cur]) return f[now][r][cur];
	if(r >= p[now]) f[now][r][cur] = std::max(f[now][r][cur] , dp(now , r - p[now] , std::max(cur , c[now])));
	if(!cur) return f[now][r][cur];
	for(int i = 0 ; i < (int)g[now].size() ; ++i)
		f[now][r][cur] = std::max(f[now][r][cur] , dp(g[now][i] , r , cur - 1) + d[now][i]);
	return f[now][r][cur];
}

int main()
{
	scanf("%d%d%d%d",&n,&m,&C,&T);
	for(int i = 1 ; i <= n ; ++i)
		scanf("%d%d",&p[i],&c[i]);
	for(int i = 1 ; i <= m ; ++i)
	{
		int x , y , k;
		scanf("%d%d%d",&x,&y,&k);
		g[x].push_back(y) , d[x].push_back(k);
	}
	for(int i = 1 ; i <= T ; ++i)
	{
		int s , dis , rem;
		bool flag = false;
		scanf("%d%d%d",&s,&rem,&dis);
		for(int j = 1 ; j <= rem ; ++j)
			if(dp(s , j , 0) >= dis)
			{
				printf("%d\n",rem-j);
				flag = true;
				break;
			}
		if(!flag)
			puts("-1");
	}
}

然后就到此为止了。。