Post 49

Veröffentlicht am

P1231 教辅的组成

题目背景

滚粗了的HansBug在收拾旧语文书，然而他发现了什么奇妙的东西。

题目描述

蒟蒻HansBug在一本语文书里面发现了一本答案，然而他却明明记得这书应该还包含一份练习题。然而出现在他眼前的书多得数不胜数，其中有书，有答案，有练习册。已知一个完整的书册均应该包含且仅包含一本书、一本练习册和一份答案，然而现在全都乱做了一团。许多书上面的字迹都已经模糊了，然而HansBug还是可以大致判断这是一本书还是练习册或答案，并且能够大致知道一本书和答案以及一本书和练习册的对应关系（即仅仅知道某书和某答案、某书和某练习册有可能相对应，除此以外的均不可能对应）。既然如此，HansBug想知道在这样的情况下，最多可能同时组合成多少个完整的书册。

输入输出格式

输入格式：

第一行包含三个正整数N1、N2、N3，分别表示书的个数、练习册的个数和答案的个数。

第二行包含一个正整数M1，表示书和练习册可能的对应关系个数。

接下来M1行每行包含两个正整数x、y，表示第x本书和第y本练习册可能对应。（1<=x<=N1，1<=y<=N2）

第M1+3行包含一个正整数M2，表述书和答案可能的对应关系个数。

接下来M2行每行包含两个正整数x、y，表示第x本书和第y本答案可能对应。（1<=x<=N1，1<=y<=N3）

输出格式：

输出包含一个正整数，表示最多可能组成完整书册的数目。

输入输出样例

输入样例#1：

1
2
3
4
5
6
7
8
9
10
11
12
13
5 3 4
5
4 3
2 2
5 2
5 1
5 3
5
1 3
3 1
2 2
3 3
4 3

输出样例#1：

1
2

说明

样例说明：

如题，N1=5，N2=3，N3=4，表示书有5本、练习册有3本、答案有4本。

M1=5，表示书和练习册共有5个可能的对应关系，分别为：书4和练习册3、书2和练习册2、书5和练习册2、书5和练习册1以及书5和练习册3。

M2=5，表示数和答案共有5个可能的对应关系，分别为：书1和答案3、书3和答案1、书2和答案2、书3和答案3以及书4和答案3。

所以，以上情况的话最多可以同时配成两个书册，分别为：书2+练习册2+答案2、书4+练习册3+答案3。

数据规模：

img

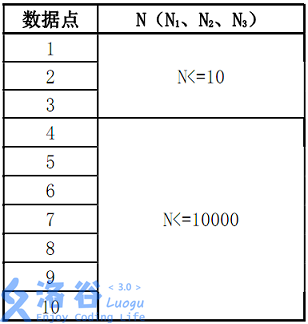
对于数据点1, 2, 3，M1，M2<= 20

对于数据点4~10，M1，M2 <= 20000

题解

果然昨天晚上状态太差了。

连建图忘记建反向边都能调一晚上。。。。

道理大家都懂，就是有时候会sb。。

这是一道网络流入门题，只不过用到了拆点的技巧来保证没个书只被使用一次。（也就是说我们在拆的点之间连个边权为一的边就能避免最后的网络最大流重复使用了一个点。

这好像是一个三分图匹配？所以比二分图多了个拆点。

Code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
// luogu-judger-enable-o2
// luogu-judger-enable-o2
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#include <queue>
#include <cstring>
#define maxn 300005
#define maxm 500005
#define INF 0x7ffffff
int hd[maxn] , ct = 1 , MaxFlow , n , n1 , n2 , n3 , m1 , m2 , dep[maxn] ,  S , T;
bool vs[maxn];
struct edge{
    int nxt , to , dis;
}e[maxm<<1];

inline void add(int x, int y , int d)
{
    e[++ct] = (edge){hd[x],y,d};
    hd[x] = ct;
}
inline void build()
{
    scanf("%d%d%d",&n1,&n2,&n3);
    scanf("%d",&m1);
    S = 0 , T = n1 * 2 + n2 + n3 + 1;
    for(int i = 1 ; i <= n2 ; ++i) //source to practice
    {
        add(S , i , 1) , add(i , S , 0);
////	   	printf("S to P EDGE : %d %d\n",S,i);
    }
    for(int i = 1 ; i <= m1 ; ++i)
    {
        int x , y;
        scanf("%d%d",&x,&y);
//		printf("P to B EDGE : %d %d\n" , y , x + n2);
        add(y , x + n2 , 1) , add(x + n2 , y , 0); // practice to book
    }
    for(int i = 1 ; i <= n1 ; ++i) // book to book
    {
        add(i + n2 , i + n2 + n1 , 1) , add(i + n2 + n1 , i + n2 , 0);
//   		printf("B part B EDGE : %d %d\n",i + n2 , i + n2 + n1);
    }
    scanf("%d",&m2);
    for(int i = 1 ; i <= m2 ; ++i)
    {
        int x , y;
        scanf("%d%d",&x,&y); // book to ans
        add(x + n2 + n1 , y + n2 + n1 * 2 , 1) , add(y + n1 * 2 + n2 ,x + n2 + n1 ,  0);
//	   	printf("B to A EDGE : %d %d\n",x + n2 + n1 , y + n2 + n1 * 2);
    }
    for(int i = 1 ; i <= n3 ; ++i) //ans to Terminal
    {
        add(i + n1 * 2 + n2 , T , 1) , add(T , i + n1 * 2 + n2 , 0);
//		printf("A to T EDGE : %d %d\n",i + n1 * 2 + n2 , T);
    }
}
inline bool bfs()
{
    for(int i = 1 ; i <= n ; ++i)	dep[i] = INF;
    dep[S] = 0;
    std::queue<int> q;
    q.push(S);
    for( ; (int)q.size() ; q.pop())
    {
        int k = q.front();
        for(int i = hd[k] ; i ; i = e[i].nxt)
            if(dep[e[i].to] == INF && e[i].dis)	dep[e[i].to] = dep[k] + 1 , q.push(e[i].to);
    }
    return dep[T] != INF;
}

int dfs(int u , int cfw)
{
    if(u == T || !cfw) return cfw;
    int flow = 0 , f;
    for(int i = hd[u] ; i ; i = e[i].nxt)
    {
        int v = e[i].to;
        if(dep[v] == dep[u] + 1 && (f = dfs(v , std::min(cfw , e[i].dis))))
        {
            flow += f;
            cfw -= f;
            e[i].dis -= f , e[i^1].dis += f;
            if(!cfw) break;
        }
    }
    return flow;
}

inline int Dinic()
{
    for( ; bfs() ; MaxFlow += dfs(S,INF));
    return MaxFlow;
}

int main()
{
    build();
    n = T;
    printf("%d\n",Dinic());
}